On the validity of statistical parametric mapping for nonuniformly and heterogeneously smooth one-dimensional biomechanical data

Abstract

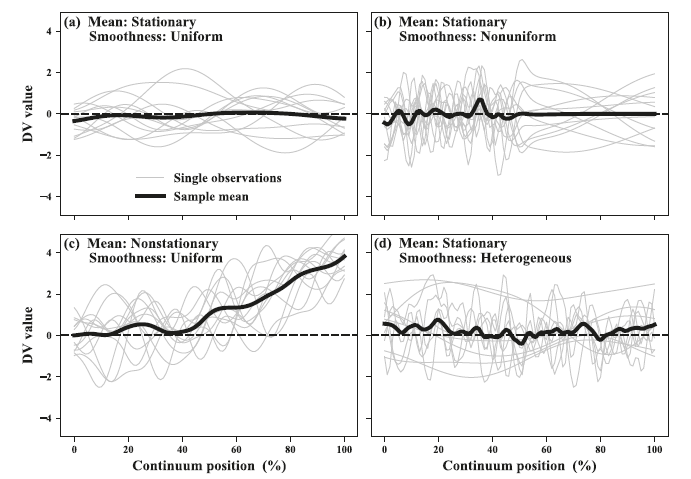
Nonuniform (non-constant) temporal smoothness can arise in biomechanical processes like impacts, and heterogeneous smoothness (unequal smoothness across observations) can arise in mechanically diverse comparisons such as padded vs. unpadded impacts, where padded dynamics are generally smoother than unpadded dynamics. It has been reported that statistical parametric mapping’s (SPM’s) probability values can be invalid for such cases. The purpose of this paper was to clarify the scope of validity for SPM analysis of nonuniformly and heterogeneously smooth one-dimensional (1D) data. We simulated a variety of nonuniformly and heterogeneously smooth Gaussian 1D data over a range of smoothness values, and computed Type I error rates across 10,000 simulation iterations for each smoothness type. Results showed that, in all cases, SPM accurately controlled error at the prescribed a ¼ 0:05. Moreover, the distribution of false positives was uniform across time, implying that all regions are equally likely to produce false positives, irrespective of local roughness. We nevertheless show that cluster-level inferences (i.e., p values specific to local regions of significance), while never exceeding alpha (by definition), may be overor-underestimated by approximately 0.01 for the currently simulated scenarios. We conclude that SPM’s null hypothesis rejection decisions are valid for both nonuniform and heterogeneous 1D data, but that clusters’ p values may be marginally too small/large in rough/smooth regions, respectively. Since cluster-level p values never exceed a, these p value errors are negligible for hypothesis testing purposes. Nevertheless, inter-cluster p value comparisons should be avoided. Implications for statistical power and general results interpretation are discussed.