Bayesian inverse kinematics vs. least-squares inverse kinematics in estimates of planar postures and rotations in the absence of soft tissue artifact

Abstract

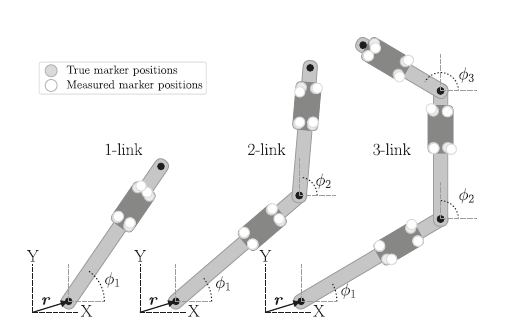
A variety of inverse kinematics (IK) algorithms exist for estimating postures and displacements from a set of noisy marker positions, typically aiming to minimize IK errors by distributing errors amongst all markers in a least-squares (LS) sense. This paper describes how Bayesian inference can contrastingly be used to maximize the probability that a given stochastic kinematic model would produce the observed marker positions. We developed Bayesian IK for two planar IK applications: (1) kinematic chain posture estimates using an explicit forward kinematics model, and (2) rigid body rotation estimates using implicit kinematic modeling through marker displacements. We then tested and compared Bayesian IK results to LS results in Monte Carlo simulations in which random marker error was introduced using Gaussian noise amplitudes ranging uniformly between 0.2 mm and 2.0 mm. Results showed that Bayesian IK was more accurate than LS-IK in over 92% of simulations, with the exception of one center-of-rotation coordinate planar rotation, for which Bayesian IK was more accurate in only 68% of simulations. Moreover, while LS errors increased with marker noise, Bayesian errors were comparatively unaffected by noise amplitude. Nevertheless, whereas the LS solutions required average computational durations of less than 0.5 s, average Bayesian IK durations ranged from 11.6 s for planar rotation to over 2000 s for kinematic chain postures. These results suggest that Bayesian IK can yield order-of-magnitude IK improvements for simple planar IK, but also that its computational demands may make it impractical for some applications.