A computational framework for estimating statistical power and planning hypothesis-driven experiments involving one-dimensional biomechanical continua

Abstract

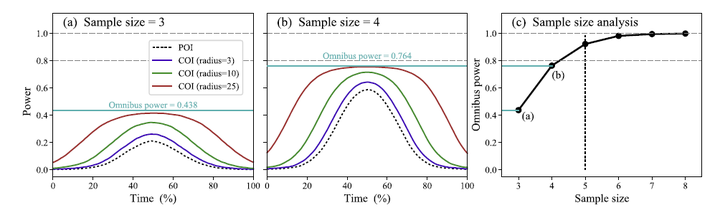
Statistical power assessment is an important component of hypothesis-driven research but until relatively recently (mid-1990s) no methods were available for assessing power in experiments involving continuum data and in particular those involving one-dimensional (1D) time series. The purpose of this study was to describe how continuum-level power analyses can be used to plan hypothesis-driven biomechanics experiments involving 1D data. In particular, we demonstrate how theory- and pilot-driven 1D effect modeling can be used for sample-size calculations for both single- and multi-subject experiments. For theory-driven power analysis we use the minimum jerk hypothesis and single-subject experiments involving straight-line, planar reaching. For pilot-driven power analysis we use a previously published knee kinematics dataset. Results show that powers on the order of 0.8 can be achieved with relatively small sample sizes, five and ten for within-subject minimum jerk analysis and between-subject knee kinematics, respectively. However, the appropriate sample size depends on a priori justifications of biomechanical meaning and effect size. The main advantage of the proposed technique is that it encourages a priori justification regarding the clinical and/or scientific meaning of particular 1D effects, thereby robustly structuring subsequent experimental inquiry. In short, it shifts focus from a search for significance to a search for non-rejectable hypotheses.