Two-way ANOVA for scalar trajectories, with experimental evidence of non-phasic interactions

Abstract

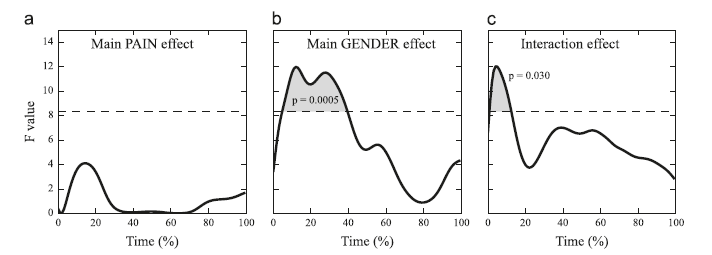
Kinematic and force trajectories are often normalized in time, with mean and variance summary statistic trajectories reported. It has been shown elsewhere, for simple one-factor experiments, that statistical testing can be conducted directly on those summary statistic trajectories using Random Field Theory (RFT). This technical note describes how RFT extends to two-factor designs, and how bizarre “non-phasic interactions” can occur in multi-factor experiments. We reanalyzed a public dataset detailing stance phase knee flexion during walking in (a) patellofemoral pain vs. controls, and (b) females vs. males using both a full model (with interaction effect) and a main-effects-only model. In both models the main effect of PAIN failed to reach significance at α¼ 0.05. The main effect of GENDER reached significance over 5–40% stance (p¼0.0005), but only for the full model. The interaction effect (in the full model) reached significance over 0–15% of stance (p¼0.030), and resulted from greater flexion in females but decreased flexion in males in PFP vs. controls. Thus there was a non-phasic interaction in which a non-significant interaction (over 20–40% stance) suppressed the main effect of GENDER. Similarly, if we had only analyzed 20–40% stance, we would have committed Type II error by failing to reject the null PAIN–GENDER interaction hypothesis. The possible presence of non-phasic interactions implies that trajectory analyses must be conducted at the whole-trajectory level, because a failure to do so will generally miss non-phasic interactions if present.